Any tree that its elements have at most two children nodes is called a binary tree. Those children nodes are referred typically as the left and the right child.
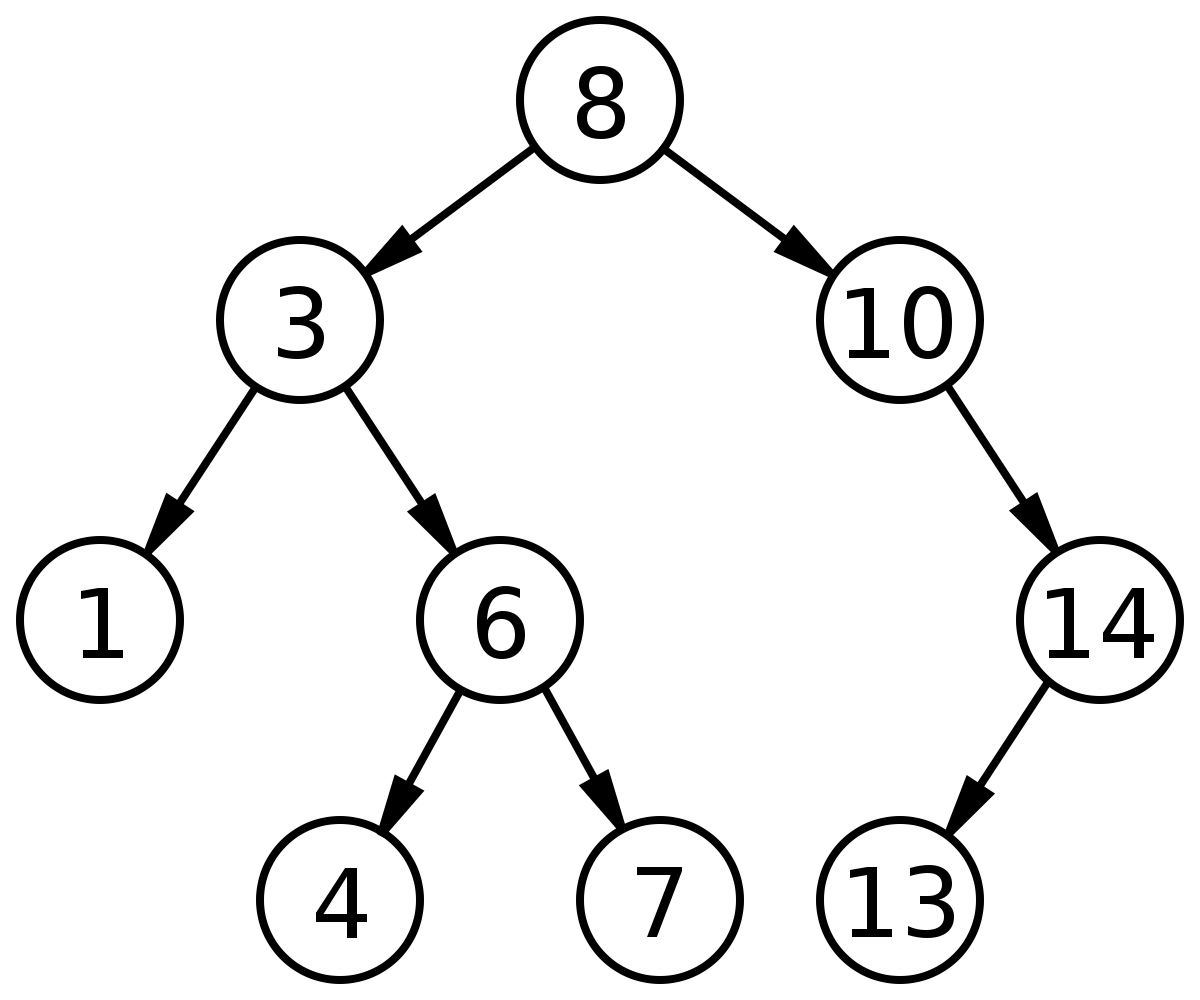
As we can see a tree is not a linear data structure and represents nodes that are connected by edges. A tree has the following properties:
- Higher-level node is marked as the Root node
- All nodes except Root are associated with one parent node
- All nodes can have an arbitrary number of children
Binary Search Tree
Binary Search Tree or BST is a tree in which all nodes follow the below rule
The left sub-tree of a node has a value lesser or equal to its parent node’s key. The right sub-tree of a node has a value greater than to its parent node’s key.
Python Implementation
If we want to implement a BST in Python we need to provide at least the following functionality:
- Initialization
- Insertion
- Traverse
- Search
Initialization
class TreeNode:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def print_tree(self):
print(self.data)We declare a class as TreeNode or Node and this will represent each node in the tree. Each tree node has three attributes:
- Data: representing the value it holds
- Left: representing a number that is lesser than the data attribute
- Right: representing a number that is greater than the data attribute
Finally, for the time being, we have a print method that only prints the value of the tree node.
We can initialize and print as the example below:
root = TreeNode(5) root.print_tree()
Insertion
In order to insert a new value to our BST, we will create an insert method. The insert method will check the value to be inserted with the parent value and it will decide if it will be added as left or right.
We will also need to update the print_tree method.
class TreeNode:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def insert(self, data):
if self.data is None:
self.data = data
else:
if data < self.data:
if self.left is None:
self.left = TreeNode(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = TreeNode(data)
else:
self.right.insert(data)
def print_tree(self):
if not self.data:
return
print(self.data)
if self.left:
self.left.print_tree()
if self.right:
self.right.print_tree()
root = TreeNode(5)
root.insert(2)
root.insert(12)
root.insert(7)
root.print_tree()In the insert method, we initially check that we have a root value. If there is not a root value then we add the given value as root to our tree. In the case where we have a root value and the value, we want to insert is lesser than the root value, we check if the left value of our parent node is none. In the case it is none then we initialize a new tree node with the given value and we store it as the left attribute of the parent. If the left attribute already exists then we recursively call the insert method and we do the same but the parent this time is the left attribute. Respectively we do the same for the right attribute if the value which we want to insert is greater than the root value.
Regarding the print method, we simply check if we have a root value initially and if not we simply return nothing. If we do have a root value we print it and then we perform the same check for the left and right attributes. Again we call the print method recursively for the attributes in order to be able to print the whole tree.
Note here that this is an unordered print and it will print the root value, then the left values and last the right values.
Typically we want to have both options available -unordered and ordered- for us in order to display the tree. We can create an in order print method and the only change that will have compared to the existing print method is the order in which we call the print statements.
class TreeNode:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def insert(self, data):
if self.data is None:
self.data = data
else:
if data < self.data:
if self.left is None:
self.left = TreeNode(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = TreeNode(data)
else:
self.right.insert(data)
def pre_order_print_tree(self):
if not self.data:
return
print(self.data)
if self.left:
self.left.pre_order_print_tree()
if self.right:
self.right.pre_order_print_tree()
def in_order_print_tree(self):
if not self.data:
return
if self.left:
self.left.in_order_print_tree()
print(self.data)
if self.right:
self.right.in_order_print_tree()
root = TreeNode(15)
root.insert(8)
root.insert(22)
root.insert(7)
root.insert(24)
root.insert(6)
root.insert(10)
root.insert(21)
root.pre_order_print_tree()
root.in_order_print_tree()This is how our implementation so far could be with the insert method and the two print methods.
The outcome of the print methods can be found below.
root.pre_order_print_tree()
15
8
7
6
10
22
21
24root.in_order_print_tree()
6
7
8
10
15
21
22
24And the created tree in this example is:
15
/ \
8 22
/ \ / \
7 10 21 24
/
6Traversing Trees
Traversal is a process to visit all the nodes of a tree. Essentially what we achieve with those two print methods is to traverse the whole tree. There are three ways to traverse a tree:
- In-order
- Pre-order
- Post-order
We already checked how to do in-order and pre-order traversals and in post-order traversal, the difference is that the root node is visited last.
Typically when we want to traverse a tree we gather the values in a list in order to use them somehow.
Let us check an implementation for the traverse methods:
def pre_order_traverse(self, root):
result = []
if root:
result.append(root.data)
result = result + self.pre_order_traverse(root.left)
result = result + self.pre_order_traverse(root.right)
return result
def in_order_traverse(self, root):
result = []
if root:
result = self.in_order_traverse(root.left)
result.append(root.data)
result = result + self.in_order_traverse(root.right)
return result
def post_order_traverse(self, root):
result = []
if root:
result = self.post_order_traverse(root.left)
result = result + self.in_order_traverse(root.right)
result.append(root.data)
return resultEach one of the methods each similar and the logic is the same as in print methods. The change is the order in which we add tree node values on our list.
Below is the outcome if we invoke each one of those methods:
print(root.pre_order_traverse(root))
[15, 8, 7, 6, 10, 22, 21, 24]print(root.in_order_traverse(root))
[6, 7, 8, 10, 15, 21, 22, 24]print(root.post_order_traverse(root))
[6, 7, 10, 8, 21, 22, 24, 15]Searching
In order to search for a value within a tree, we need to compare the value that we want to search with the existing nodes. We will traverse the nodes from left to right and the same will happen recursively for each node. If the value exists in the tree we will find it as the parent in the respective node we will be traversing at this point. In this implementation, we simply return string messages if the value has or has not been found.
def find_value(self, value_to_find):
if value_to_find < self.data:
if self.left is None:
return str(value_to_find)+' not found'
return self.left.find_value(value_to_find)
elif value_to_find > self.data:
if self.right is None:
return str(value_to_find)+' not found'
return self.right.find_value(value_to_find)
else:
return(str(self.data) + ' found')Example method calls and outcomes:
print(root.find_value(7))
7 foundprint(root.find_value(33))
33 Not FoundComplete Implementation
Complete code of what we have talked about in this post can be found below:
class TreeNode:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def insert(self, data):
if self.data is None:
self.data = data
else:
if data < self.data:
if self.left is None:
self.left = TreeNode(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = TreeNode(data)
else:
self.right.insert(data)
def pre_order_print_tree(self):
if not self.data:
return
print(self.data)
if self.left:
self.left.pre_order_print_tree()
if self.right:
self.right.pre_order_print_tree()
def in_order_print_tree(self):
if not self.data:
return
if self.left:
self.left.in_order_print_tree()
print(self.data)
if self.right:
self.right.in_order_print_tree()
def pre_order_traverse(self, root):
result = []
if root:
result.append(root.data)
result = result + self.pre_order_traverse(root.left)
result = result + self.pre_order_traverse(root.right)
return result
def in_order_traverse(self, root):
result = []
if root:
result = self.in_order_traverse(root.left)
result.append(root.data)
result = result + self.in_order_traverse(root.right)
return result
def post_order_traverse(self, root):
result = []
if root:
result = self.post_order_traverse(root.left)
result = result + self.in_order_traverse(root.right)
result.append(root.data)
return result
def find_value(self, value_to_find):
if value_to_find < self.data:
if self.left is None:
return str(value_to_find)+" Not Found"
return self.left.find_value(value_to_find)
elif value_to_find > self.data:
if self.right is None:
return str(value_to_find)+" Not Found"
return self.right.find_value(value_to_find)
else:
return(str(self.data) + ' is found')
root = TreeNode(15)
root.insert(8)
root.insert(22)
root.insert(7)
root.insert(24)
root.insert(6)
root.insert(10)
root.insert(21)
root.pre_order_print_tree()
root.in_order_print_tree()
print(root.pre_order_traverse(root))
print(root.in_order_traverse(root))
print(root.post_order_traverse(root))
print(root.find_value(7))
print(root.find_value(33))
print(root.find_value(15))
print(root.find_value(98))Regarding the time complexity of search and insert operations, the worst-case scenario is that we may have to travel from the top to the bottom which makes the time complexity equal to O(n) where n is the height of the given tree.
One of the most complex operations we may have to perform is the deletion due to the possibilities that exist in this scenario (Node is a simple leaf without children, Node has one child, Node has two children).
Both deletion and optimization will be discussed in a future post.